WEKTORYDawno, dawno temu, kiedy świat był dużo młodszy, a ludzie szczęśliwsi, pojawiły się komputery. Najpierw nieśmiało, potem coraz odważniej zaczęły wkraczać we wszystkie sfery życia człowieka, wychodząc z laboratoriów szalonych matematyków i trafiając - jak by powiedział wieszcz pod strzechy. Nie wszyscy byli przekonani do nowej zabawki, musiała więc ona zaprezentować się od najlepszej strony. Magicy, zwani informatykami, postanowili, że komputery powinny przede wszystkim ładnie wyglądać. Przebiegli ci ludzie nie ograniczyli się do opakowania swoich ulubieńców w ładne, kolorowe pudełka, ale zmusili je do tego, żeby pokazywały rzeczy, jakich nie sposób obejrzeć na kartce papieru, w kinie, czy też w telewizji. Pojawiła się cała masa bardzo kolorowych obrazków, do których oglądania potrzebne były komputery... Konserwatyści odpowiedzieli na to stwierdzeniem, że do oglądania ładnych obrazków nie są potrzebne żadne wyszukane zabawki. W pewnym sensie mieli rację; informatycy potrzebowali nowego pomysłu, który mógłby zamknąć usta "niewiernym". I wymyślili: pojawiła się grafika wektorowa! Z terminem tym zetknąłem się już bardzo dawno temu i nie ukrywam, że od razu bardzo mnie zainteresował, a właściwie - zaintrygował. Nie wiedziałem, jak należy go rozumieć! Kiedy dorosłem i zostałem studentem matematyki, zacząłem męczyć różnych mądrych ludzi, prosząc ich o wyjaśnienie tajemnicy grafiki wektorowej. Niestety, nikt nie chciał wytłumaczyć jej tak, żeby dało się to pojąć. Poszedłem więc do bibliotek i znalazłem kilka książek, które rozjaśniły mi w głowie. Zrozumiałem! Teraz chciałbym podzielić się tą wiedzą z Wami. Zakładam, że rozumiecie, co to jest płaszczyzna, punkt, układ współrzędnych prostokątnych i inne tego typu pojęcia. Zacznijmy od czterech punktów, położonych na płaszczyźnie w taki sposób, jak na obrazku w sąsiedniej kolumnie. Oprócz punktów możecie zobaczyć dwa odcinki oraz fragment krzywej. Umówmy się, że zestaw złożony z punktów i odcinków (tak naprawdę są to wektory, ale nie musimy chwilowo o tym pamiętać) nazwiemy wielobokiem charakterystycznym Beziera (to nazwisko francuskiego matematyka, który "wynalazł" grafikę wektorową), a fragment krzywej - segmentem. Dodatkowo, punkty x0 i x3 nazwijmy węzłami, zaś x1 i x2 - punktami kontrolnymi. Łatwo się przekonać, że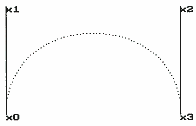 
wielobok charakterystyczny jednoznacznie określa kształt segmentu krzywej. Sprawa wygląda tak: załóżmy, że mamy wielobok charakterystyczny i chcemy na jego podstawie narysować segment krzywej. Wiemy, że taki segment składa się z punktów i na pewno istnieje punkt leżący w jednej trzeciej długości segmentu krzywej. Weźmy odcinek x0x1 i znajdźmy punkt leżący w jednej trzeciej jego długości (oznaczmy go y01). To samo zróbmy z odcinkiem x1x2 (punkt oznaczmy y12), a następnie z odcinkiem x2x3 (punkt oznaczmy y23). Zbudujmy teraz odcinki y01y12 i y12y23 i wykonajmy na nich analogiczną operację (otrzymane punkty oznaczmy odpowiednio z1 i z2). Kiedy zbudujemy odcinek z1z1, to okaże się, ze punkt leżący w jednej trzeciej jego długości jest poszukiwanym punktem, należącym do segmentu krzywej. Opisaną operację możemy powtórzyć n razy, zawsze dzieląc odcinki na n części. Na wszystkich rysunkach krzywą podzielono na 80 części, aby otrzymane wykresy były w miarę gładkie. Zmniejszenie n spowoduje ułatwienie obliczeń, ale jednocześnie spowoduje gorszy wygląd krzywej.Oczywiście, kiedy do kreślenia krzywych wektorowych zatrudnimy komputer, to łatwo przekonamy się, że on robi to szybciej i lepiej. Kiedy jeszcze spróbujemy przemieszczać wszystkie punkty wieloboku charakterystycznego, to zobaczymy, jak silnie wiążą one krzywą. Dosłownie każdy ruch spowoduje zmianę jej kształtu. Dla ułatwienia załóżmy, że nie będziemy zmieniać położenia węzłów, a jedynie punktów kontrolnych. Spróbujmy przemieścić w lewo punkt x1. Zobaczmy, co z tego wynika...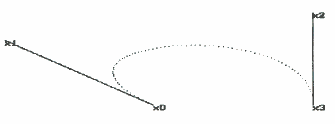 
Gdyby komuś chciało się sprawdzać, to zobaczy, że nie ma tu żadnego oszustwa - wszystko jasno wynika z położenia punktów wieloboku! Zauważmy, że z matematycznego punktu widzenia taka operacja jest bardzo prosta - wszelkie przekształcenia operują zawsze tylko na czterech punktach, bo przecież narysowanie krzywej jest czynnością trywialną - to już umiemy!Zobaczmy, co dalej... 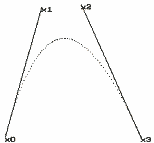 Ładne? Nie takie rzeczy umiemy. Co powiecie na odrobinę poplątania z pomieszaniem? 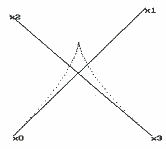 Jak zauważyliście, wszystkie operacje dotyczyły tylko fragmentu krzywej. W przypadku, gdy chcemy operować na bardzo skomplikowanych kształtach, musimy całość podzielić na kawałeczki, do których bez obaw możemy zastosować sprawdzone (patrz powyżej) metody postępowania. Po co to wszystko? Jak to? Przecież to oczywiste! Jeśli prosty kształt możemy przedstawić czterema, a bardziej skomplikowany - n razy czterema punktami, to wystarczy tylko napisać proste procedurki, aby bardzo rozbudowane obrazki zapisywać w postaci niewielkich plików. Na świecie (na dużych komputerach) się tak robi! Może by tak spróbować? Może by tak mały programik graficzny z grafiką wektorową? A gdyby tak jeszcze w przestrzeni? Być może kiedyś, jeśli czas pozwoli, porozmawiamy o przestrzennych wektorach. To dopiero zabawa... (hed)
|
Powrót na start | Powrót do spisu treści | Powrót na stronę główną